1.
Sосн = πR² = 4π, значит R²=4 ⇒ R=2 ⇒ D=4
Sсеч = D*h = 4h =8/π, значит h = 2/π
Sб.п. = 2πRh = 2π*2*2/π = 8
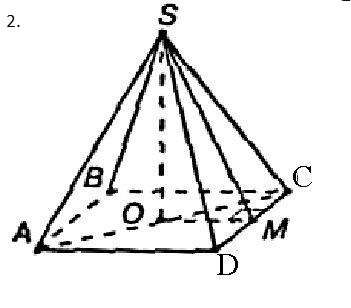
2. рисунок приложен
Диагональное сечение это треугольник ACS с высотой SO, равной высоте пирамиды и основанием АС, являющийся диагональю квадрата ABCD.
AC = AB√2 = 6√2*√2 = 12
Так диагональное сечение равновелико основанию получаем
1/2*SO*AC = AB²
1/2*SO*12 = (6√2)²
6*SO = 72
SO = 12
Так как в основании квадрат Sосн = АВ² = 72
V = 1/3*Sосн*h
V = 1/3*72*12 = 288
3. Рисунок в вложении
Vконуса = 1/3*πHR²
H - катет АВ
R - катет АС
Катет, лежащий против угла в 30° равен половине гипотенузы
АС = 4√3/2 = 2√3
АВ = 4√3*sin30 = 4√3*√3/2 = 2*3 = 6
V = 1/3*3*6*(2√3)² = 6*12 = 72
4.
V = πR²h
Sосн = πR² = 9π, значит R²=9 ⇒ R=3 ⇒ D=6
Sсеч = D*h = 6h =12/π, значит h = 2/π
V = π*9*2/π = 18
5. SO = AB (по условию)
AS = 3√5 (по условию)
АО = АВ/2 = R
из треугольника ASO по теореме Пифагора
AS² = AO²+SO²
(3√5)² = АВ²/4+АВ
5АВ²/4 = 45
АВ²/4 = 9
АВ² = 36
АВ = 6
АО = 6/2 = 3 = R