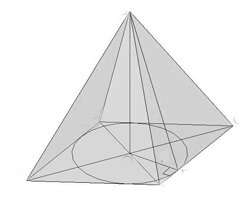
Площадь повер пирамиды равна площадь основания+площадь граней *4
Площадь ромба 1/2*d1*d2= 24( где d= диагонали)
Если двугранные углы равны то в основание(ромб) можно вписать окружность, и вычислить её радиус
г=s осн/p, где p - полупериметр
Вычисляем сторону ромба в основании. Диагонали пересекаются под прямым углом и образуют 4 прямоугольных треугольника со сторонами 3 и 4 см( половины диагоналей) Следовательно сторона ромба( гипотенуза) будет по теореме Пифагора 5 см. Периметр-20, полупериметр-10см
r=2,4
Вычисляем гипотенузу прямоугольного треугольника, образованного высотой пирамиды(1-й катет) и радиусом окружности"2-й катет по теореме Пифагора : под корнем( 1^2+2,4^2)=2,6
Эта гипотенуза будет высотой h другого треугольника, который является гранью пирамиды/ Сторона-основание этого треугольника- 5 см(сторона ромба)
Площадь треугольника( ребра) =1/2*сторона в основании* h=6,5
Площадь всех граней=26
Площадь пирамиды =26+24+50 см кв