--- 1 ---
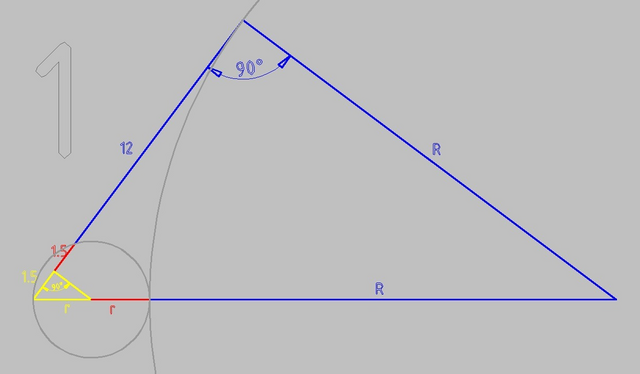
на рисунке 1 маленький жёлтый треугольник подобен большому синему
т.к. один угол общий, второй прямой
r/1.5 = (2r + R)/(12 + 3)
r/1.5 = (2r + R)/15
10r = 2r + R
R = 8r
--- 2 ---
Теорема Пифагора для большого синего треугольника
15² + R² = (2r + R)²
15² + (8r)² = (2r + 8r)²
15² + 64r² = 100r²
15² = 36r²
5² = 4r²
r² = (5/2)²
r = 5/2
R = 8r = 20
--- 3 ---
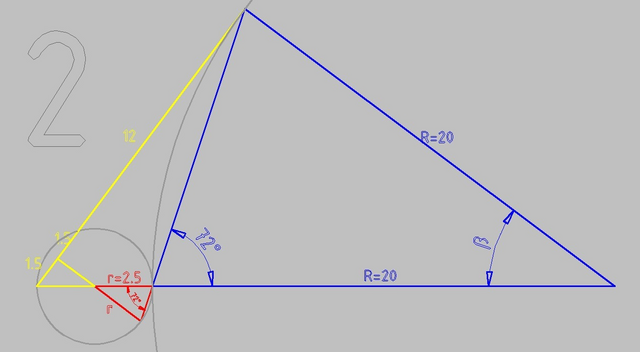
рисунок 2
Синий и красный треугольники подобны - оба они равнобедренные, и углы при основаниях равны как вертикальные
--- 4 ---
угол при вершине β можно найти из большого прямоугольного треугольника со сторонами 15, 20 и 2r + R = 2*2.5 + 20 = 25
sin(β) = 15/25 = 3/5
--- 5 ---
Высота красного треугольника, проведённая к боковой стороне
h = 2.5*sin(β) = 2.5*3/5 = 7.5/5 = 1.5
--- 6 ---
Основание искомого треугольника 2R = 40
Высота равна высоте маленького красного на рис 2
h = 1.5
Площадь
S = 1/2*40*1.5 = 20*1.5 = 30
------
Примечание
На картинке кажется, что изображены касательные к двум окружностям, и к маленькой и к большой. Но для циферок в 3 и 12 такое невозможно. В итоге касательная только одна, к большой окружности.