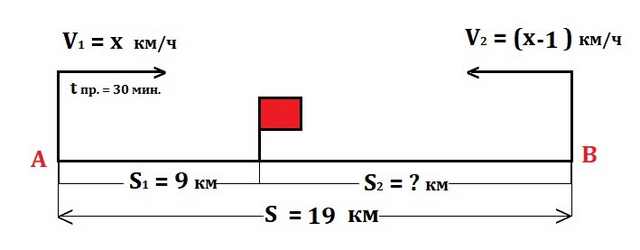
Турист, вышедший из п.А :
Расстояние S₁ = 9 (км )
Скорость V₁ = x (км/ч)
Время в движении t₁ = 9/x (ч.)
Время привала t пр. = 30 мин. = 30/60 часа = 0,5 (ч.)
Время на путь до момента встречи t₁ + t пр. = 9/х + 0,5 (ч.)
Турист, вышедший из п.В :
Расстояние S₂ = 19 - 9 = 10 (км)
Скорость V₂ = x - 1 (км/ч)
Время на путь до момента встречи t₂ = 10/(x - 1) (ч.)
Так как туристы вышли навстречу друг другу одновременно, то затратили на путь до момента встречи равное количество времени:
t₁ + t пр. = t₂ ⇒ уравнение:
9/х + 0,5 = 10/(х - 1)
знаменатели не равны 0 ⇒ х≠0 ; х≠ 1
9/х + 1/2 = 10/(х - 1)
(18 + х) / 2х = 10/(х - 1)
решим, как пропорцию :
(18 + х)(х - 1) = 2х * 10
18x - 18 +x² -x = 20x
x² + 17x - 18 - 20x = 0
x² - 3x - 18 = 0
D = (-3)² - 4*1*(-18) = 9 + 72 = 81 = 9²
D>0 - два корня уравнения
х₁ = ( - (-3) - 9) /(2*1) = (3 - 9)/2 = -6/2 = - 3 не удовлетворяет условию задачи, т.к. скорость - неотрицательная величина
х₂ = ( - (-3) + 9) /(2*1) = (3 + 9)/2 = 12/2 = 6 (км/ч) скорость туриста, вышедшего из пункта А
Ответ : 6 км/ч .