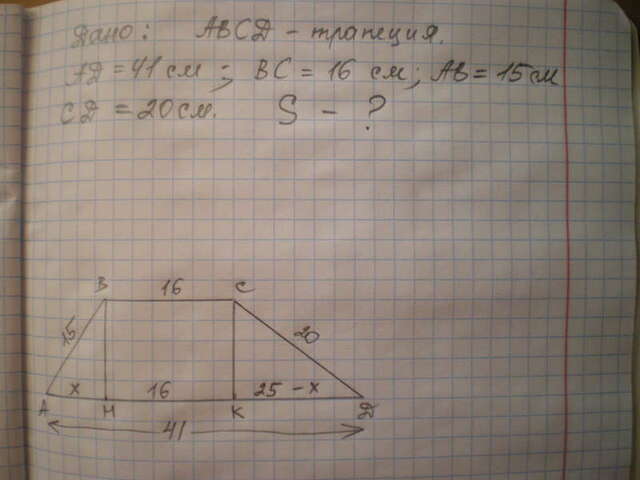
Опустим из вершин углов при основании ВС высоты ВН и СК к АД. Высоты разделили основание АД на три отрезка.
Обозначим отрезок АН=х
Отрезок КН = ВС=16 см , поэтому отрезок КД=41-16-х=25-х
Найдем квадрат высоты ВН (СК) из прямоугольных треугольников, примыкающих к боковым сторонам, где эти стороны - гипотенузы.
ВН²=АВ²-х²
СК²=СД²-(25-х)²
АВ²-х²=СД²-(25-х)²
225-х²=400 - (625-50х+х²)
225-х² =400- 625+50х -х²
50х=450
х=9
АН=9 см, ВН=12 см (египетский треугольник)
S=(16+41):2*12=342 cм²