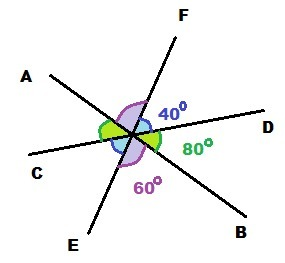
Прямые AB, CD и EF пересекаются в точке О. ∠BOD=80°, ∠FOD:∠BOE=2:3. Найдите меньший из углов AOF, AOC и COE
Решение:
∠BOD = 80°; ∠FOE - развернутый, равен 180°
∠FOE - ∠BOE = 180° - 80° = 100° = ∠FOD + ∠BOE
∠FOD : ∠BOE = 2 : 3 ⇒ ∠FOD = (2/3) * ∠BOE
∠FOD + ∠BOE = 100°
(2/3) * ∠BOE + ∠BOE = 100°
(5/3)*∠BOE = 100°
∠BOE = 100° * 3/5 = 60°
∠FOD = (2/3) * ∠BOE = (2/3) * 60° = 40°
Вертикальные углы равны ⇒
∠AOF = ∠BOE = 60°
∠AOC = ∠BOD = 80°
∠COE = ∠FOD = 40°
Из углов 60°, 80°, 40° наименьший ∠COE = 40°
Ответ: 3) 40°
В задаче есть ещё одно условие : "Один из углов прямой, два другие относятся как 4:5". На рисунке видно, что прямых углов нет, и что никакие углы в сумме не могут дать прямой угол, поэтому данное условие считаю типографской ошибкой.