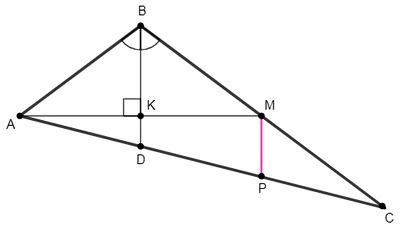
BD является высотой и биссектрисой в △ABM, следовательно и медианой.
AK=KM =AM/2 =1
Доп. построение:
MP||BD, P∈AC
MP - средняя линия в △BCD (BM=MC, AM - медиана)
MP=BD/2 =1/2
DK - средняя линия в △PAM (AK=KM)
DK=MP/2 =1/4
BK= BD-DK = 1 -1/4 =3/4
△BKM - египетский треугольник (BK=3/4; KM=4/4), множитель 1/4
BM=5/4
BC=2BM =5/2 =2,5