F'(x)=1/2+cosx
f'(x)=0
cosx=-1/2
x=+-arccos(-1/2)+2πn=+-(π-arccos(1/2))+2πn=+-(π-π/3)+2πn
=+-(2/3)π+2πn, n∈Z
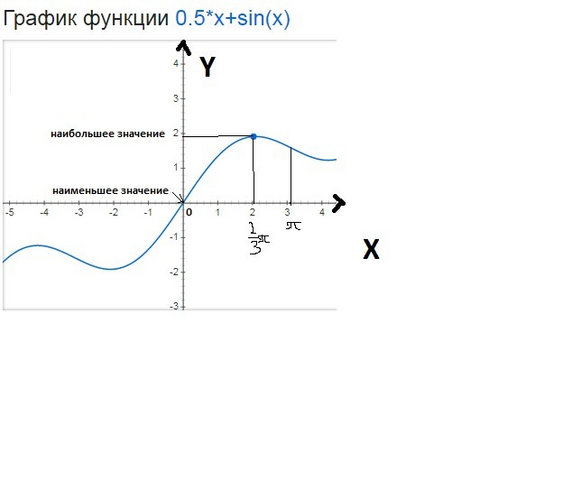
из этого множества решений отрезку [0;π] принадлежит только х=(2/3)π
вычислим значение функции на концах отрезка и в точке экстремума
f(0)=0+sin0=0
f(2π/3)=(1/2)*(2π/3)+sin(2π/3)=π/3+√3/2 ≈3,14/3+1,73/2≈1,04+0,86=1,9
f(π)=(1/2)π+sinπ=π/2+0=π/2 ≈3,14/2=1,57
наименьшее значение 0
наибольшее значение π/3+(√3)/2