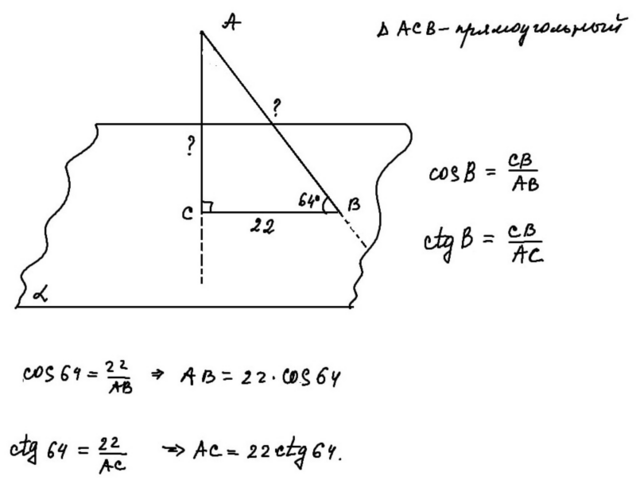
Получается прямоугольный треугольник (смотри рисунок).
Через тригонометрические функции находим гипотенузу и катет. Это наклонная и перпендикуляр соответственно.
Если нужны точные вычисления, то оставляешь так, как решено на рисунке.
Если нужны приблизительные значения, то по таблицам находишь приблизительные значения косинуса и котангенса 64° и умножаешь на 22.
Дано: АС⊥α, СВ=22, ∠В=64°. (если вы построили рисунок, и все точки назвали, то в дано можно эти названия сразу указать и коротко всё записать, т.к. СВ -это и есть проекция. угол В - это угол между наклонной и плоскостью)
Найти: АВ, АС
Решение: т.к. прямая АС перпендикулярна плоскости α, то она перпендикулярна любой прямой, лежащей в этой плоскости.
Значит АС⊥СВ.
ΔАВС - прямоугольный. Используем тригонометрические функции для того, чтобы найти гипотенузу и катет прямоугольного треугольника.
(а дальше с приложенного файла)