Решить неравенство 3^(x^2) * 5^(x-1)≥3

Question

Решить неравенство 3^(x^2) * 5^(x-1)≥3

Comments

откуда пример?

---

x>=1

---

https://znanija.com/task/28646127

Answer 1

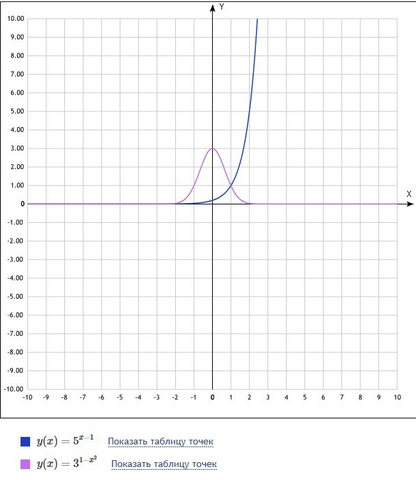
5^(x-1)>=3^(1-x^2)
решу сначала равенство логарифмированием по основанию 3
(x-1)log(3)5=1-x^2
x^2+xlog(3)5-log(3)5-1=0
получила квадратное уравнение относительно х
D=(log(3)5)^2+4(1+log(3)5)=(log(3)5+2)^2
x1=(-log(3)5+log(3)5+2)/2=1
x2=(-log(3)5-log(3)5-2)/2=-log(3)5-1
Методом интервалов  ++++-1-log(3)5--------1+++++
Ответ:x=(-беск;-1-log(3)5)U[1;+беск)

---

Comments

один промежуток потеряли

---

(-oo;-log3(15)]

---

если поиграть с масштабом графика, то и потерянный промежуток был бы виден ))

---

сомневалась я на счет второго корня из-за графика)

---

да, лучше бы я его не строила....