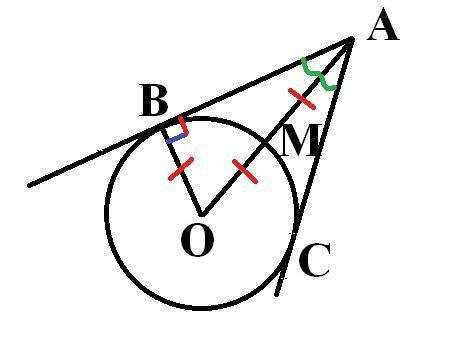
Пусть АВ и АС - касательные из точки А к окружности с центром в О.
Пусть М - точка пересечения отрезка АО и АМ. Тогда АМ - кратчайшее расстояние от А до окружности. По условию АМ = ОМ = ОВ = r, где r - радиус окружности.
По ствойству касательной к окружности ОВ⊥АВ ⇒ ΔАОВ - прямоугольный, в котором гипотенуза ОА в 2 раза больше катета ОВ ⇒ ∠ОАВ = 30°.
Как известно, центр окружности, вписанной в угол, лежит на биссектрисе этого угла. Поэтому ∠ВАС = 2·30° = 60°.
Ответ: 60°.