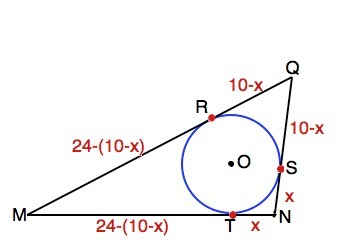
Задача по теме об отрезках касательных из одной точки.
Отрезки касательных, проведенных к окружности из одной точки, от общей точки до точек касания равны друг другу.
Примем ТN=x.
Тогда NS=TN=x,
SQ=QN-SN=10-x
QR=QS=10-x
MR=MQ-QR=24-(10-x)
MT=MR=24-(10-x)=14+x
МN=MT+TN =>
20=14+x+х
2х=6
х=3 =>
TN=3 (ед. длины)