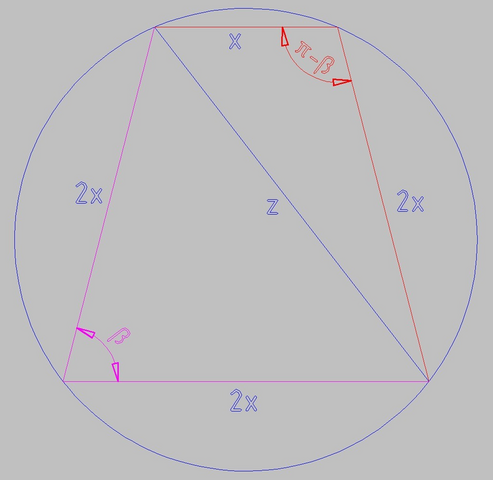
Трапеция равнобокая, противоположные углы в сумме дают π
По теореме косинусов для треугольника ниже диагонали
z² = (2x)² + (2x)² - 2*2x*2x*cos(β)
z² = 8x² - 8x²*cos(β)
По теореме косинусов для треугольника выше диагонали
z² = (2x)² + x² - 2*2x*x*cos(π-β)
z² = 5x² + 4x²*cos(β)
---
8x² - 8x²*cos(β) = 5x² + 4x²*cos(β)
3x² = 12x²*cos(β)
3 = 12*cos(β)
1 = 4*cos(β)
cos(β) = 1/4
sin(β) = √(1-cos²(β)) = √(1-1/16) = √(15/16) = √15/4
По теореме синусов, для треугольника ниже диагонали, R - разиус описанной окружности, причём окружность одна и та же и для трапеции, и для каждого из двух рассматриваемых треугольников
z/sin(β) = 2R
z/(√15/4) = 4*8
z = 4√15 см
Это ответ.