4)
∠АВС - вписанный, он равен половине центрального ∠АОС.
Пусть
х это величина ∠АВС, тогда
2х это величина ∠АОС
По условию их сума равна 36°, получим уравнение:
х + 2х = 36°
3х = 36°
х = 36° : 3
х = 12°
∠АВС = 12°
∠АОС = 12° · 2 = 24°
Ответ: ∠АОС = 24°
6 задача.
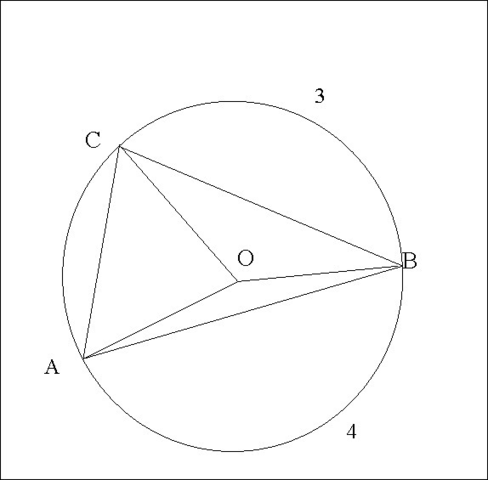
1)∠АОВ - центральный, опирается на дугу ∪АВ, поэтому ∪АВ = 160°.
2)По условию ∪АВ содержит 4 части, а ∪ВС состоит из 3-х частей.
Находим величину дуги ∪ВС.
∪ВС = 160° : 4 · 3 = 120°
3)Находим величину третьей дуги ∪АС.
В сумме эти три дуги образуют окружность, величина которой 360°.
∪АВ + ∪ВС +∪АС = 360°
∪АС = 360° - 160° - 120° = 80°
4) Самая маленькая дуга ∪АС, на неё опирается ∠АВС, который и будет меньшим углом треугольника ΔАВС.
∠АВС - вписанный, он равен половине дуги АС.
∠АВС = 80° : 2 = 40°.
Ответ: 40°