4)
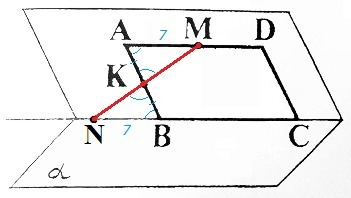
Плоскость ABC и плоскость α пересекаются по прямой BC. Все общие точки этих плоскостей принадлежат прямой BC. Прямая MK лежит в плоскости ABC. Точка пересечения MK и плоскости α лежит на BC - точка N.
AK=BK
∠AKM=∠BKN (вертикальные)
∠MAK=∠NBK (накрест лежащие при AD||BC)
△AKM=△BKN (по стороне и прилежащим к ней углам)
AM=BN =14/2 =7
AD=BC=14 (противоположные стороны параллелограмма)
NC=BN+BC =7+14=21
5)
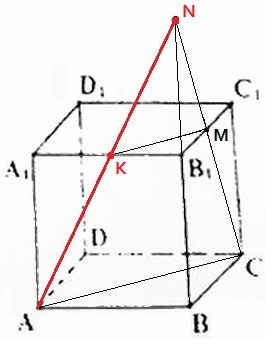
1) (CBB1) и (BAA1) пересекаются по прямой BB1.
CM лежит в плоскости CBB1 и пересекает BB1 в точке N.
2) (AMC) и (BAA1) имеют общие точки A и N, следовательно имеют общую прямую AN.
3) AN лежит в плоскости BAA1 и пересекает A1B1 в точке K.