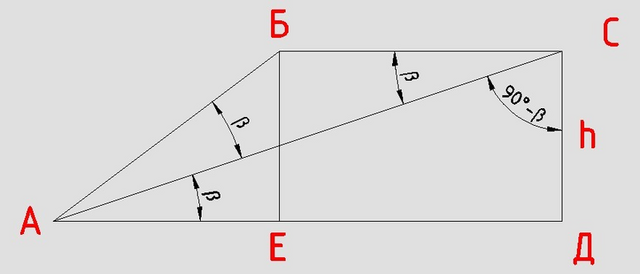
Пусть острый угол равен 2β
тогда
∠САД = ∠САБ = β
∠АСД = 90°-β
∠БСА = 90° - ∠АСД = 90° - (90°-β) = β
Треугольник АБС равнобедренный :)
Высота трапеции h, тогда
h = 9*tg(β)
h = 5*sin(2β)
---
h² = 81*sin²(β)/cos²(β)
h² = 25*4*sin²(β)*cos²(β)
---
81*sin²(β)/cos²(β) = 100*sin²(β)*cos²(β)
81/100 = cos⁴(β)
Извлекаем корень
положительный
cos²(β) = +9/10
Это хорошо, позже будем решать дальше
cos²(β) = -9/10
Это плохо, дальше не развиваем
cos²(β) = 9/10
sin²(β) = 1-cos²(β) = 1-9/10 = 1/10
h² = 100*sin²(β)*cos²(β)
h² = 100*1/10*9/10
h² = 9
h = 3 (снова отбросили отрицательный корень)
Ну и площадь
S = 1/2(9+5)*3 = 21 см²