Площадь прямоугольника можно вычислить по формуле
S=a•b, где а и b- его стороны.
Прямоугольник - четырехугольник.
Площадь четырехугольника можно вычислить по формуле
S=d1•d2•sinα:2, где d1 и d2 - диагонали, α - угол между ними.
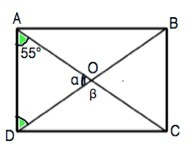
Диагонали прямоугольника равны, точкой пересечения делятся пополам. Эти равные половинки со сторонами прямоугольника образуют равнобедренные треугольники.
∠ВDA=∠CAD=55° (дано).⇒
Сумма углов треугольника 180°⇒
α=∠АОD=180°-(∠OAD+∠ODA)=70°
S(ABCD)=AC•DB•sin70°:2
S(ABCD)=4•4•0,9397°:2 ≈ 7,518 см²
-----------------------
Тот же результат получим, если для решения возьмем смежный с углом α угол β.