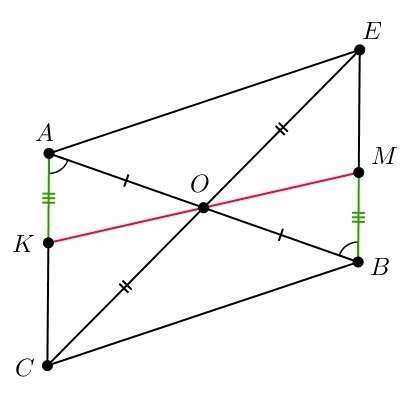
Рассмотрим четырёхугольник AEBC (см. рисунок). Его диагонали в точке пересечения делятся пополам, следовательно, это параллелограмм.
У параллелограмма противоположные стороны параллельны. Значит, ∠KAO = ∠MBO (накрест лежащие углы при параллельных прямых AC и EB и секущей AB).
Рассмотрим треугольники KAO и MBO. У них AK=MB, AO=OB, ∠KAO = ∠MBO. Поэтому они равны (по двум сторонам и углу между ними). Следовательно, KO=OM как соответствующие стороны. Что и требовалось доказать.