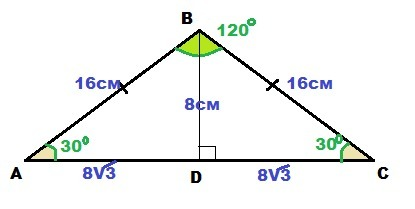
В треугольнике может быть только один тупой угол, поэтому угол 120° - это угол при вершине
ΔABC - равнобедренный, ∠ABC = 120°; AB = BC = 16 см
1 способ.
BD - высота, медиана и биссектриса ⇒
BD⊥AC; AD = DC; ∠ABD = ∠CBD = ∠ABC/2 = 120°/2 = 60°
ΔABD - прямоугольный, ∠ADB=90°; ∠ABD = 60°
Катет прямоугольного треугольника равен гипотенузе, умноженной на синус противолежащего угла:
AD = AB * sin∠ABD = 16*√3/2 = 8√3 см
Периметр:
P = 16 + 16 + 2*8√3 = 32 + 16√3 см
2 способ. Теорема косинусов
AC² = AB² + AC² - 2AB*AC*cos∠ABC =
= 16² + 16² - 2*16*16*cos120° =
= 512 - 512*(-1/2) = 512 + 256 = 768
AC = √768 = 16√3 см
Периметр:
P = 16 + 16 + 16√3 = 32 + 16√3 см