Y = (2x +3)/(x² -9)
x² - 9 ≠ 0, ⇒ x² ≠ 9,⇒ x≠ +-3
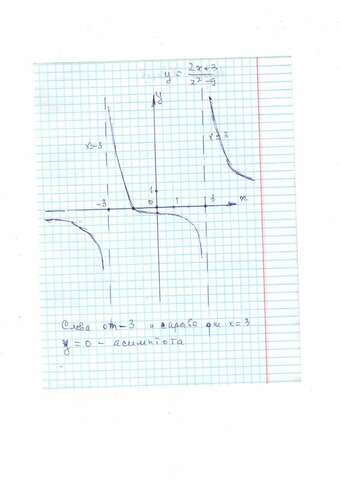
вывод: х = 3 и х = -3 вертикальные асимптоты
График нашей функции рвётся на 3 части. Одна слева от х = -3, другая в "полосе" между х = -3 и х = 3, и третья справа от х =3
y' = (2(x² - 9) - 2x +3)*2x)/(x² -9)² = (-2x² -6x -18)/(x² -9)² < 0
Вывод: наша функция убывающая на всей области определения.
( т.е. график на координатной плоскости , все его 3 куска, "ползёт" вниз)
график нашей функции имеет пересечение с осью х:
у = 0 при 2х +3 = 0, ⇒ х = -1,5
Вывод: Имеем точку (-1,5; 0)
график нашей функции имеет пересечение с ось. у:
х = 0 при у = (0+3)/(0 -9) = -1/3
Вывод: Имеем точку (0; -1/3)
Можно строить график. см. в приложении.