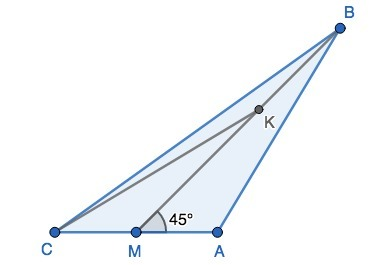
Обозначим AM = MC = x, MK = a, AB = CK = b.
Если ∠AMB = 45°, то ∠CMK = 180° - 45°, так как эти углы смежные.
Теорема косинусов для треугольника AMB:
AM^2 + MB^2 - 2 AM MB cos∠AMB = AB^2
x^2 + (a + 1)^2 - √2 x (a + 1) = b^2
Теорема косинусов для треугольника CMK:
CM^2 + MK^2 - 2 CM MK cos∠CMK = CK^2
x^2 + a^2 + √2 x a = b^2
Приравниваем выражения для b^2:
x^2 + (a + 1)^2 - √2 x (a + 1) = x^2 + a^2 + √2 x a
√2 x (a + a + 1) = (a + 1)^2 - a^2
√2 x (2a + 1) = 2a + 1
√2 x = 1
x = 1/√2
Тогда AC = 2x = √2