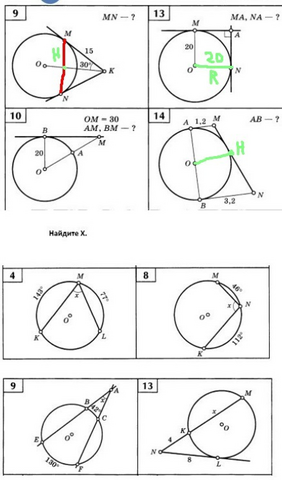
№9
Проведи MN , получиться треугольник MHK(Поставишь точку H на прямой KO)
1)Треугольник прямоугольный, значит МH = 1/2 × MK ;
2)MH = HN = 7.5
3)MN = MH + HN = 7.5 + 7.5 = 15
Отсюда можно догадаться что △MNK - Равносторонний
№10
Зная сторону ВO и OM можем найти сторону BM(Прямоугольный треугольник) ;
1)BM² = OM² - BO² = 900 - 400 = √500 = 10√5
2)Т.к Радиус(BO) = 20 , тогда BO = AO = 20
3)AM = OM - OA = 30 - 20 = 10
№13
Свойства касательных: MA = NA:
МO = ON = 20, а т.к ON ⊥ AN(Свойство), значит ∠MON = ∠ONA = ∠NAM = ∠AMO. Значит это квадрат. Все стороны равно 20.
№14
Средняя линия равна:
1)(AM+BN)/2 = (1.2 + 3.2) / 2 = 2.2(OH)
2)OH - Радиус окружности (O;r), а так как AO и OB тоже радиусы, тогда
AO = OB = OH
3)AB = AO + OB = 2.2 + 2.2 = 4.4
================================================================
№4
360° - 143° -77° = 140°
Дуга KL равна 140°, напротив неё лежит ∠KML
Так как угол не центральный:
∠KML = Дуга KL / 2 = 140° / 2 = 70°
x = 70°
№8
Так же как и в задаче (№4)
1) 360° - 46° - 112° = 202° (Дуга MK)
Т.к ∠KMN не центральный, тогда:
2) x = Дуга MK / 2 = 202° / 2 = 101°
№9
Угол, образованный двумя секущими окружность прямыми равен полуразности заключенных между его сторонами дуг.
x = 1/2 (130°- 42°)= 88° / 2= 44°
№13
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.
NL² = NM × NK ;
8² = (4+x) × 4 ;
64 = 16 + 4x ;
48 = 4x ;
x = 12