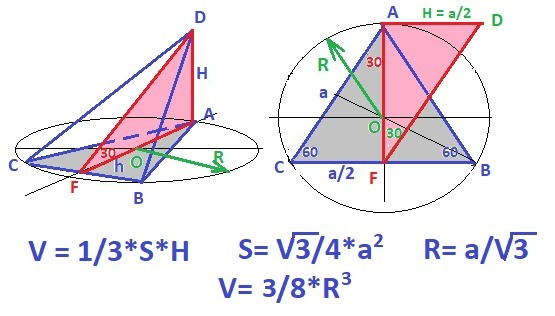
ДАНО
R = 3 см - радиус описанной окружности
∠САВ = α = 60°- угол при вершине
АВ = АС - равнобедренный треугольник в основании.
∠AFD = β = 30°- двугранный угол
НАЙТИ:
V = ? - объём пирамиды
РЕШЕНИЕ (думаем, вспоминаем, находим).
1) Объём пирамиды по формуле:
V = 1/3*S*H, где:S - площадь основания, Н - высота пирамиды.
2) Если угол при вершине равнобедренного треугольника равен 60°, то и два других угла равны 60° - это правильный треугольник.
3) Радиус описанной окружности для правильного треугольника:
R = a/√3, где: а - сторона правильного треугольника (в основании).
Отсюда находим формулу для стороны:
a = √3*R - (пока не вычисляем)
4) Площадь правильного треугольника по формуле:
S = √3/4*a².
Подставили значение - а.
a² = 3*R²
S = 3/4*√3*R² - площадь основания.
5) Переходим к рисунку 2. Развернем ΔADF в плоскость основания - ΔАВС.... и получаем параллелограмм ADFC, так как..
а) ∠CAD = 30°+90° = ∠CFD
б) AC = DF
в) AD = CF = а/2 = √3/2*R = H - высота пирамиды.
6) Подставим в формулу 1)

- (немного устали даже писать такую формулу)
7) Подставили известное значение R =3:
V = 3/8*R³ = 3/8*3³ = 3/8*27 = 81/8 = 10 1/8 = 10.125 см³ - объём - ОТВЕТ
ВЫВОД:
Хороший математик старается писать формулы, а потом уж и вычислять только нужные значения.