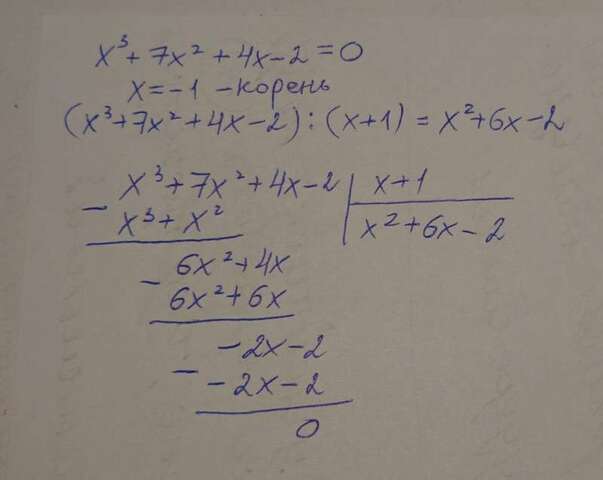X³ + 7x² + 4x - 2 = 0
x³ + (x² + 6x²) + (6x - 2x) - 2 = 0
x³ + x² + 6x² + 6x - 2x - 2 = 0
x²(x + 1) + 6x(x + 1) - 2(x + 1) = 0
(x + 1)(x² + 6x - 2) = 0
Произведение равно нулю, если одни из множителей равен нулю.
1) x + 1 = 0
x = -1
2) x² + 6x - 2 = 0
D = 36 -4 * (-2) = 44
√D = √44 = 2√11
x₁ = (-6 - 2√11)/2 = -3 - √11
x₂ = (-6 + 2√11)/2 = √11 - 3
Ответ: -1; -3 - √11; √11 - 3
*на множители можно разложить и с помощью деления на многочлен. Несложно заметить, что x=-1 - корень уравнения. Поэтому исходное выражение можно разделить на (x + 1). Столбик во вложении.