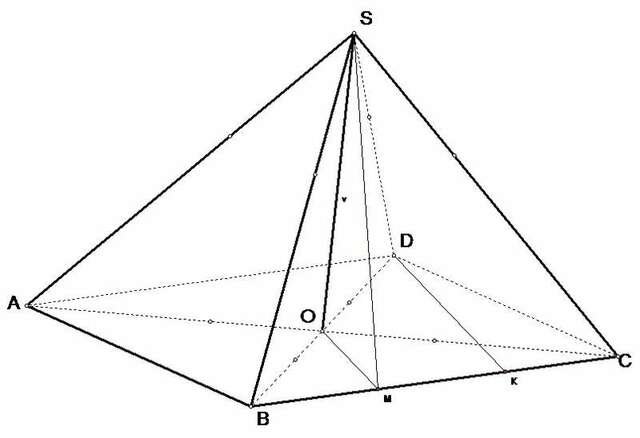
Если боковые грани наклонены к основанию пирамиды под одним и тем же углом, то высота приходит в центр вписанной окружности. В параллелограмм можно вписать окружность, если он ромб.
Стороны ромба равны по 24√3/4 =6√3 см. Площадь его находим по формуле а²*sin 120=36*3*√3/2 = 54√3.
Высоты боковых граней равны. Их можно найти из ΔSOM. SM=OM/cos 60°.
OM - половина высоты ромба,DK= DC* sin∠C= 6√3*√3/2 =9 см. ОМ= 4,5 см.
SM= 4,5/(/2) = 9 см.
S(бок) =1/2*P(осн) * SM = 1/2*24√3*9 =108√3.
Полная поверхность равна 108√3+54√3=162√3. Значит а=162.