1) В основании пирамиды прямоугольник со сторонами 4см и см. Две боковые грани...

Question

1) В основании пирамиды прямоугольник со сторонами 4см и см. Две боковые грани перпендикулярны основанию, и образуют с основанием угол 30 и 45 градусов. Вычислите площадь поверхности пирамиды.
2) В правильной усечённой четырёхугольной пирамиде стороны основания равны 5 и 9 см.Двугранный угол при большем основании равен 45 градусов.Вычислите объём усеченной пирамиды.

Comments

Очень интересно получается у вас в условии первой задачи! Вами сказано, что боковые грани перпендикулярны основанию (я понимаю так, что угол между каждой такой гранью и основанием равен по 90°). И тут же, в продолжении, пишите, что эти грани образуют с основанием углы 30° и 45°. Как такое возможно? Коллеги, помогите! )))

Answer 1

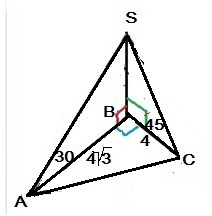
1.S авс=1/2*4*4√3=8√3 см²
SB=ВС=4, так как ΔSBC-равнобедренный.
S sbc=1/2*4*4=8 см²
S asb=1/2*4√3*4=8√3 см²
AC=√((4√3)²+4²)=8 см
AS=2SB=2*4=8 см (SB-катет против угла 30°=1/2 гипотенузы)
SC=√(4²+4²)=√32=4√2 см
ΔASC-равнобедренный, AS=AC
h ΔASC к стороне SC:
h=√(8²-(2√2)²)=√(64-8)=2√14 см
S asc=1/2*2√14*4√2=4√28=8√7 см²
S полн=8+8√3+8√3+8√7=8(1+2√3+√7) см²
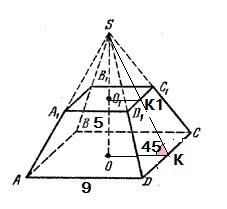
2. V ус. пир.=1/3h(Sниж.+√ (Sниж.*Sверх.)+ Sверх) 
Основания пирамиды- квадраты, поэтому
Sнижн=9*9=81 см²
Sверх=5*5=25 см²
ΔSOK-равнобедренный, так как ∠SKO=45°, значит 
h=OO1=SO-SO1=4,5-2,5=2cм
V=1/3*2*(81+√(81*25)+25)=2/3*(81+45+25)=302/3≈100,67

---

---