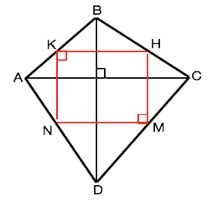
Диагонали делят четырехугольник на треугольники, в которых отрезки, соединяющие середины боковых сторон, – средние линии, поэтому параллельны и равны половинам оснований этих треугольников, т.е. равны половинам диагоналей ABCD. .
В ∆ АВС и ∆ ADC отрезки КН=MN=AC:2=6
В ∆ ABD и СBD отрезки KN=HM=BD:2=7,5
Противоположные стороны четырехугольника KHMN параллельны диагоналям исходного АВСD и между собой. Так как АС и ВD взаимно перпендикулярны, то соседние стороны KHMN также перпендикулярны. ⇒
KHMN – прямоугольник.
Площадь прямоугольника равна произведению длин соседних сторон.
S (KHMN)=KH•HM=6•7,5=45 см²