Срочно!!! 100 Баллов! В треугольнике ABC провели медиану BM. Оказалось, что сумма углов A...

Question

Срочно!!! 100 Баллов!
В треугольнике ABC провели медиану BM. Оказалось, что сумма углов A и C равна углу ABM. Найдите отношение BC:BM.

Comments

задача не для всех

Answer 1

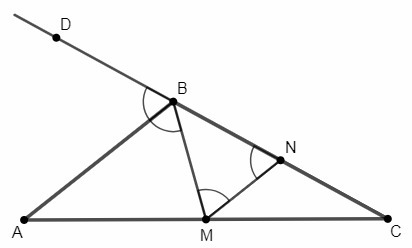
Внешний угол треугольника (∠ABD) равен сумме внутренних углов, не смежных с ним.
∠ABD= ∠A+∠C
∠ABM= ∠A+∠C (по условию)
∠ABD=∠ABM

Построим среднюю линию MN в △ABC.
AB||MN, BN=BC/2

∠ABM=∠BMN (накрест лежащие при параллельных AB||MN)
∠ABD=∠BNM (соответственные при параллельных AB||MN)
∠BMN=∠BNM, △BMN - равнобедренный, BM=BN

BM=BC/2

Ответ: BC/BM =2

---

Comments

И какое именно отношение BC:BM

---

из последней строки не видно?

---

0,5 не подходит

---

1 к 2

---

бред

---

Спрашивайте.

---

Скажите, пожалуйста, какое отношение Bc к BM в десятичной нумерации

---

BC:BM =2

---

BM - половина ВС

---

спасибо