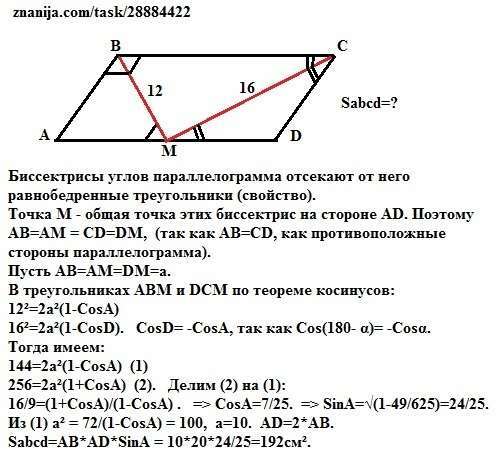
Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники (свойство).
Точка М - общая точка этих биссектрис на стороне AD.
Поэтому АВ=АМ=CD=DM, (так как АВ=СD, как противоположные стороны параллелограмма).
Пусть АВ=AM=DM=a.
В треугольниках АВМ и DCM по теореме косинусов:
12²=2a²(1-CosA)
16²=2a²(1-CosD). CosD= -CosA, так как Соs(180- α)= -Cosα.
Тогда имеем:
144=2a²(1-CosA) (1)
256=2a²(1+CosA) (2). Делим (2) на (1):
16/9=(1+CosA)/(1-CosA) . => CosA=7/25. => SinA=√(1-49/625)=24/25.
Из (1) а² = 72/(1-CosА) = 100, а=10. AD=2*AB.
Sabcd=AB*AD*SinA = 10*20*24/25=192см².