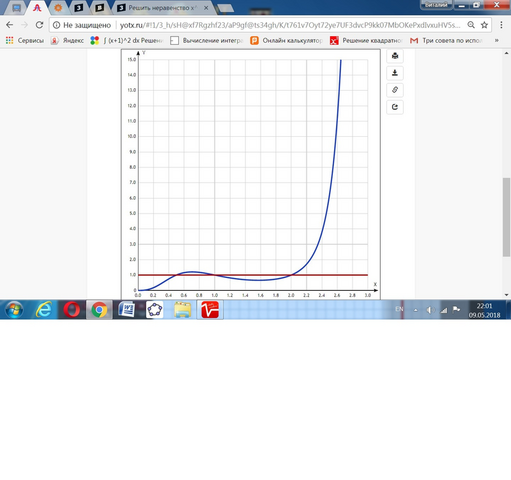
Дано неравенство x^(2x^2-5x+2) > 1.
Любое неотрицательное число в степени больше 0 больше 1.
Разложим показатель степени:
2x^2-5x+2 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-5)^2-4*2*2=25-4*2*2=25-8*2=25-16=9;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(2root9-(-5))/(2*2)=(3-(-5))/(2*2)=(3+5)/(2*2)=8/(2*2)=8/4=2;x_2=(-2root9-(-5))/(2*2)=(-3-(-5))/(2*2)=(-3+5)/(2*2)=2/(2*2)=2/4=0.5.
Можно записать:
2x^2-5x+2 = 2(х - 2)(х - (1/2)) = (х - 2)(2х - 1).
Заданное неравенство: х^((x - 2)(2x - 1) > 1.
Записываем условия:
x > 0,
x - 2 > 0, x > 2,
2x - 1 > 0, x > (1/2).
2 точки разрыва функции: х = 2 и х = 1/2.
Ответ:
(1/2) < x < 2,
x > 2.