ДАНО
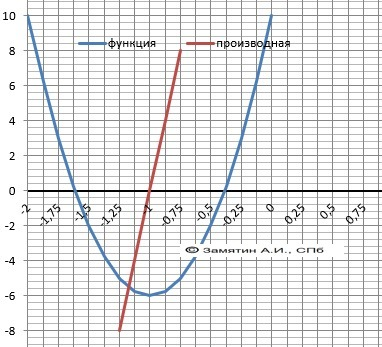
Y(x)
= 16*x² + 32*x
1.Область
определения D(x) - Х∈(-∞;+∞)
- непрерывная.
Вертикальной асимптоты нет.
2.
Пересечение с осью Х. Y=0 при х = - 0,387, - 1,612.
Положительна
- X∈(-∞;-1,6)∪(-0,38;+∞),
отрицательна - X∈(-1,612;-0,387).
3. Пересечение
с осью У. У(0) = 100.
4. Поведение
на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞
Горизонтальной асимптоты нет.
5.
Исследование на чётность.Y(-x) ≠ - Y(x).
Функция общего вида.
6.
Производная функции.Y'(x)= 32*x +32 = 32*(x+1).
Корни
при Х= - 1.
7.
Локальные экстремумы.
Минимум – Ymin(-1)=-6.
8.
Интервалы возрастания и убывания.
Возрастает
- Х∈[-+;+∞],
убывает = Х∈(-∞;-6].
8.
Вторая производная - Y"(x) = 32
Точки перегиба нет.
9.
Вогнутая – «ложка» во всем интервале определения.
10.
График в приложении.
ДАНО
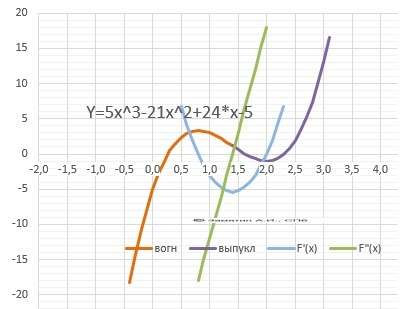
Y(x)
= 5x³ - 21*x² + 24*x - 5.
1.Область
определения D(x) - Х∈(-∞;+∞)
- непрерывная.
Вертикальные асимптоты - нет.
2.
Пересечение с осью Х. Y=0 при х = 0,266, 1,63, 2,31.
Положительна
- X∈(0,266;1,63)∪(2,31;+∞),
отрицательна - X∈(-∞;0,266)∪(1,633;2,31).
3. Пересечение
с осью У. У(0) = -5.
4. Поведение
на бесконечности.limY(-∞) = -∞ limY(+∞) = +∞
5.
Исследование на чётность.Y(-x) ≠ - Y(x).
Функция ни чётная ни нечётная - общего вида.
6.
Производная функции.Y'(x)= 15*x² - 42*х + 24
Корни производной:
при Х= 0,8 и 2.
7.
Локальные экстремумы.
Максимум
Ymax(0,8)= 3,32, минимум – Ymin(2)=-1.
8.
Интервалы возрастания и убывания.
Убывает
- Х∈[0,8;2], возрастает = Х∈(-∞;0,8]∪[2;+∞).
8.
Вторая производная - Y"(x) = 30*x - 42 =0.
Корень
производной - точка перегиба Y"(x)= 0,16.
9.
Выпуклая “горка» Х∈(+∞;0,16),
Вогнутая – «ложка» Х∈(0,16;+∞).
10.
График в приложении.