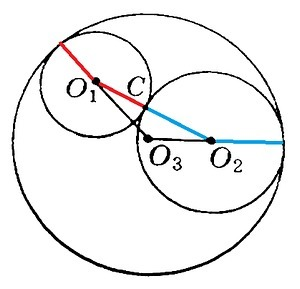
Точка касания двух окружностей лежит на прямой, проходящей через их центры.
Обозначим радиусы соответственно центрам.
Если окружности касаются внешним образом (O1,O2), растояние между их центрами равно сумме радиусов.
O1O2= R1+R2
Если окружности касаются внутренним образом (O3,O1; O3,O2), растояние между их центрами равно разности большего и меньшего радиусов.
O3O1= R3-R1
O3O2= R3-R2
Периметр треугольника равен сумме расстояний между центрами =2R3
-------------
С данными числами не выполняется неравенство треугольника (сумма двух сторон треугольника больше третьей стороны).
Треугольник со сторонами 12, 7, 5 не существует.