Помогите решить задание, исследовать функцию и построить ее график. Пожалуйста))) **...

Question

Дан 1 ответ

mefody66_zn · Answer 1 · 2018-05-31T06:44:47+0000

$y= \frac{x}{5}*ln(e^2+ \frac{3}{x} )$
1) Область определения:
{ x ≠ 0
{ e^2 + 3/x > 0
При x > 0 левая часть положительна. При x < 0
-3/x < e^2
x < -3/e^2 ~ -0,406
Область определения: x ∈ (-oo; -3/e^2) U (0; +oo)
2) Пересечений с осью Oy нет. Пересечение с осью Ox:
ln (e^2 + 3/x) = 0
e^2 + 3/x = 1
3/x = 1 - e^2
x = 3/(1 - e^2) = -3/(e^2 - 1) ~ -0,469
3) Периодичность - нет. Четность - не четная и не нечетная.
4) Точки разрыва. Вертикальные асимптоты.
x = -3/e^2 ~ -0,406, y стремится к +oo.
5) Критические точки. Производная равна 0.
$y'= \frac{1}{5}*ln(e^2+ \frac{3}{x} )+ \frac{x}{5} * \frac{1}{e^2+3/x}*(- \frac{3}{x^2} )=\frac{1}{5}ln(e^2+ \frac{3}{x} )- \frac{3}{5}* \frac{1}{xe^2+3} =0$
$ln(e^2+ \frac{3}{x} )- \frac{3}{xe^2+3}=0$
Я не знаю, как такое решать, но Вольфрам Альфа показывает, что при у этого уравнения корней нет. Значит, экстремумов у функции нет.
6) Промежутки возрастания и убывания функции.
При x < -3/e^2 левая часть производной положительна. Функция возрастает.
При x > 0 левая часть производной отрицательна. Функция убывает.
7) Точки перегиба. Вторая производная равна 0.
$y''=(\frac{1}{5}ln(e^2+ \frac{3}{x} )- \frac{3}{5}* \frac{1}{xe^2+3})'= \frac{1}{5} *\frac{1}{e^2+3/x}(- \frac{3}{x^2} ) - \frac{3}{5} *(- \frac{e^2}{(xe^2+3)^2} )=$
$=- \frac{3}{5} *\frac{1}{xe^2+3} ( \frac{1}{x} - \frac{e^2}{xe^2+3} ) =- \frac{3}{5} *\frac{1}{xe^2+3}* \frac{xe^2+3-xe^2}{x(xe^2+3)} =- \frac{9}{5}*\frac{1}{x(xe^2+3)^2}$
Эта дробь не может равняться 0 ни при каком x.
Точек перегиба нет.
При x < 0, будет y'' > 0, функция выпуклая вниз.
При x > 0 будет y'' < 0, функция выпуклая вверх.
8) Наклонные и горизонтальные асимптоты.
f(x) = kx + b
$k= \lim_{x \to \infty} \frac{y}{x} =\lim_{x \to \infty} \frac{1}{5}*ln(e^2+ \frac{3}{x} ) =\frac{1}{5}*ln(e^2+ 0 ) = \frac{2}{5}$
$b=\lim_{x \to \infty}(y-kx)=\lim_{x \to \infty}(\frac{x}{5}*ln(e^2+ \frac{3}{x} )- \frac{2x}{5} ) =\frac{1}{5}* \frac{3}{e^2}$
Опять же, решить этот предел мне помог Вольфрам Альфа.
Наклонная асимптота
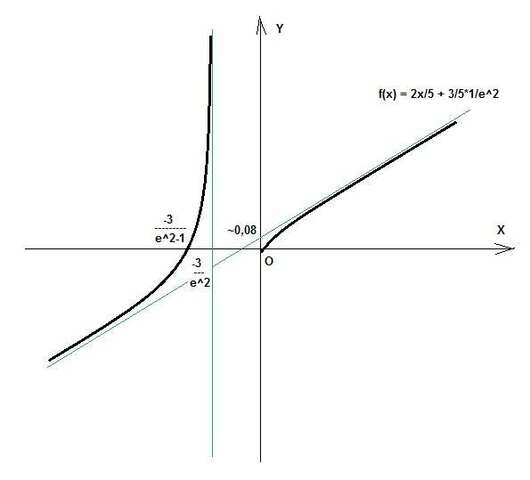
f(x) = 2x/5 + 3/5*1/e^2 ~ 0,4x + 0,08
9) Предел справа при x стремящемся к 0
$\lim_{x \to 0+0} \frac{x}{5}*ln(e^2+ \frac{3}{x})= 0$
10) Примерный график вы видите на рисунке.