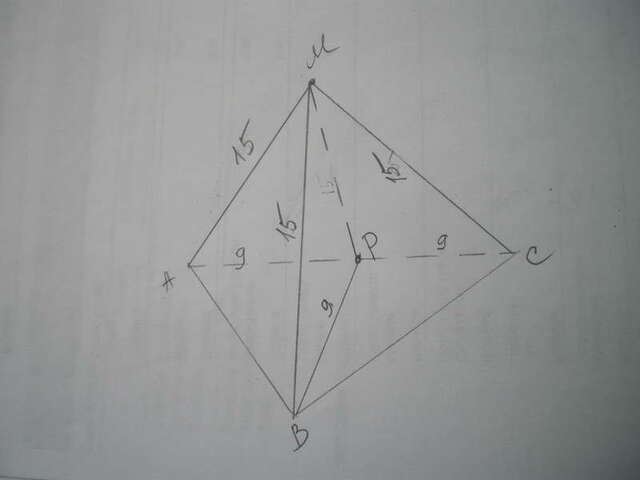
Дано: Δ АВС - прямоугольный, АС=18 см, АМ=ВМ=СМ=15 см.
Найти МР.
В прямоугольном треугольнике центр описанной окружности находится на середине гипотенузы, точка М проецируется туда же. АР=СР=ВР=18:2=9 см.
Для нахождения расстояния между точкой М и плоскостью треугольника рассмотрим Δ ВМР - прямоугольный, ∠ВРМ=90°.
МР=√(ВМ²-ВР²)=√(225-81)=√144=12 см.
Ответ: 12 см.