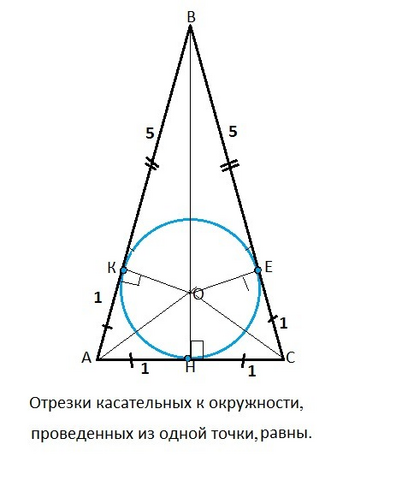
Отрезки касательных к окружности, проведенных из одной точки, равны.Рассмотрим рисунок, данный в приложении. Как равные отрезки из одной точки, ВК=ВЕ=5 смАК=АН=4 смЦентр окружности лежит на биссектрисе угла, радиус и касательная - перпендикулярны, ⇒ точка касания окружности и основания треугольника - основание высоты, которая в равнобедренном треугольнике еще и биссектриса и медиана. Следовательно, НС=НА=СЕ=4Периметр треугольника равен сумме отрезков, на которые окружность в точках касания делит его стороны. Р=10+4=14 смНаверное так