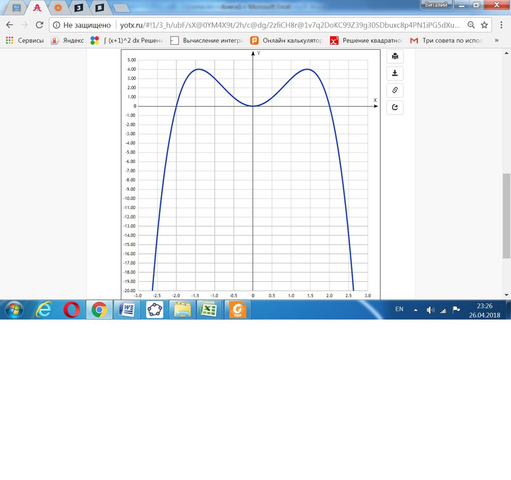
Дана функция у = -х⁴ + 4х².
а) y' = -4x³ + 8x.
б) Приравниваем y' =0.
-4x³ + 8x = -4x(x² - 2) = 0.
Получаем 3 критические точки:
х = 0, х = -√2 и х = √2.
Найденные
точки выставляются на числовой прямой. На промежутках находим знаки производной .
Где производная положительна - функция возрастает, где
отрицательна - там убывает. Точки, в которых происходит смена знака и есть
точки экстремума - где производная с плюса меняется на минус - точка максимума,
а где с минуса на плюс - точки минимума.
x = -2
-1,41421
-1
0
1 1,414214 2
y' =
16
0
-4 0 4 0 -16.
Имеем 4 промежутка монотонности:
(-∞; -√2), (-√2; 0), (0; √2) и (√2; +∞).
Функция возрастает на промежутках (-∞; -√2) и (0; √2).
убывает (-√2; 0) и (√2; +∞).
в) Из вышеприведенной таблицы находим точки экстремума:
х = -√2 и х = √2 - максимум,
х = 0 - минимум.
Экстремумы функции находим, подставив эти значения в уравнение функции:
у(макс) = 4, у(мин) = 0.
г) Находим значения х при у = 0.
-х⁴ + 4х² = 0,
-х²(х² - 4) = 0.
Получаем 3 точки: х = 0, х = 2 и х = -2.
Наименьшая из них хo = -2.
Уравнение касательной в этой точке y = y'(xo)(x - (xo) + y(xo).
y'(-2) = -4*(-2)³ + 8*(-2) = 32 - 16 = 16.
y(-2) = 0.
Уравнение касательной у = 16(х + 2) + 0 = 16х + 32.
д) На промежутке {-1; 1] имеем максимум при х = -1 и х =1 у = 3, минимум при х = 0 у = 0.
е) график дан в приложении.