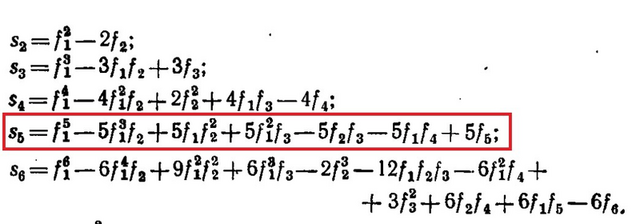См скриншот - используем предпоследнюю формулу
Имеем x^6 - 4x^5 + 0x^4 + 3x^3 - 4x^2 + x + 1 = 0
где
a0 = 1,
a1 = 1
a2 = - 4
a3 = 3
a4 = 0
a5 = - 4
a6 = 1
f1 = - a5/a6 = 4
f2 = a4/a6 = 0
f3 = - a3/a6 = - 3
f4 = a2/a6 = - 4
f5 = - a1/a6 = - 1
f6 = a0/a6 = 1
Следовательно, имеем
4^5 + 5*4^2*(-3)-5*(4)*(-4)+5*(-1) = 859