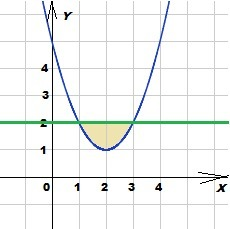
у = 2
График функции : прямая линия, параллельная оси ОХ, проходящая через точку (0; 2)
у = (х - 2)²
+ 1
График функции : квадратичная парабола с вершиной в точке (2;1),
ветви направлены вверх.
Точки пересечения графиков:
(x - 2)² + 1 = 2
x² - 4x + 4 + 1 - 2 = 0
x² - 4x + 3 = 0
Корни уравнения по теореме Виета x₁ = 3; x₂ = 1
Площадь снизу ограничена параболой g(x) = (х - 2)²+1,
сверху ограничена прямой f(x) = 2.
Обе функции непрерывны.
Область интегрирования x ∈ [1; 3]

Ответ: