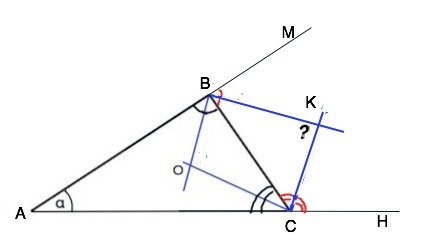
а) Сумма углов треугольника 180°. Пусть угол А в ∆ АВС=α
(∠В+∠С+∠А)-∠А=180°-α
Биссектрисы делят ∠В и ∠С пополам.
Сумма половин углов В и С равна половине их суммы (180°-α):2=90°-α/2
Из суммы углов треугольники
∠ВОС=180°- (90-α/2)=90°+α/2 – угол между биссектрисами углов В и С.
б) ВК и СК - биссектрисы внешних ∠МВСи ∠ВСН треугольника АВС.
Углы АВМ и АСН развернутые и равны 180°. Биссектрисы смежных углов делят их пополам.
(АВС+МВС):2=180°:2=90°
Аналогично угол ОСК=90°
В четырехугольнике ОВКС сумма всех углов 360°(свойство), а прямых углов В и С равна 180°.
Следовательно, угол ВКС=360°-180-угол ВОС=180°-(90+α/2)=90-α/2