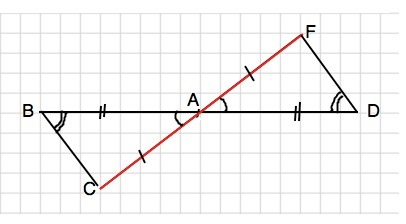
По условию в треугольниках ВAС и FAD стороны АВ=AD, AC=AF. Углы при т.А равны как вертикальные.
Δ ВAС=ΔFAD равны по 1 признаку равенства треугольников.
Тогда ∠В=∠D, ∠С=∠F. Эти пары углов - накрестлежащие.
ВD и CF- секущие при прямых ВС и FD. Если при пересечении двух прямых секущей накрестлежащие углы равны, то эти прямые параллельны. ⇒
ВС║DF . Доказано.