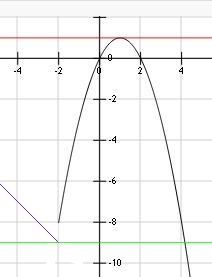
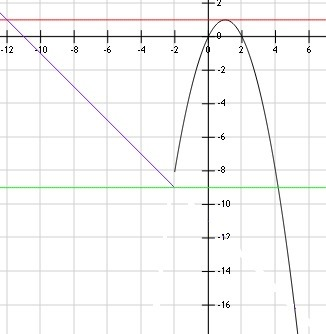
Y= -x²+2x, x > -2 в основе- парабола ветви вниз,
вершина
х₀=-b/(2a) =-2/-2=1
y₀= -1²+2=1
у= -х-11, х≤-2 луч х∈(-∞; -2]
пересекает точки (-11;0) и (-2; -9)
2 общие точки
при m=1 х∈(-12; 1)
-х-11=1
-х=12
х=-12
при m=-9 x∈(-2; 4,16)
-x²+2x=-9
-x²+2x+9=0
D=4+36=40
x₁=(-2+2√10)/-2 ≈ -2,16 (не удовлетворяет условию х > -2)
x₂=(-2-2√10)/-2 ≈ 4,16
Ответ: прямая y=m имеет с графиком ровно 2 общие точки :
при m=1 х∈(-12; 1)
при m=-9 x∈(-2; 4,16)