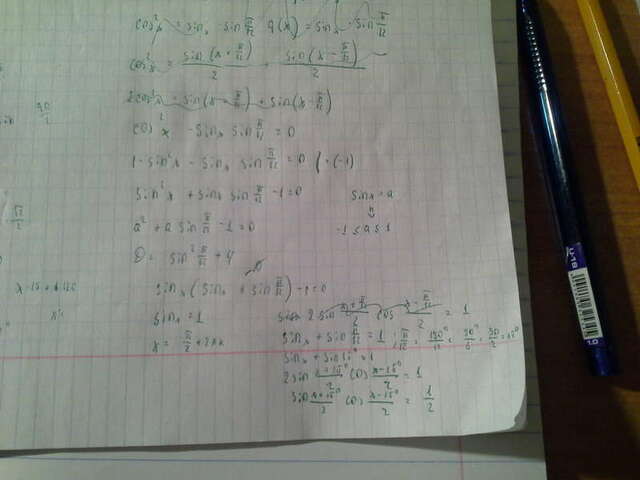Сначало перестави правое выражение на лево, потом по осн. тригоном. тождеству представил косинус квадрат как 1 минус синус квадрат, после выделил синус икс из обоих выражений, единиццу перетащил на право, приравнял к единице синус икс получил корни пи на два плюс два пи,ка , вторую скобку преобразовал по формуле сложения синусов, перетащил в право двойку и там получилось синус того на косинус этого равно 1/2, и чтобы получить из произведения синуса на косинуса 1/2 мы должны подставить такой икс чтобы получилось sin30*cos60 или sin45*cos45, но так как такого икса нету эту скобку отбрасываем.
Ответ: пи/2 + 2*пи*k