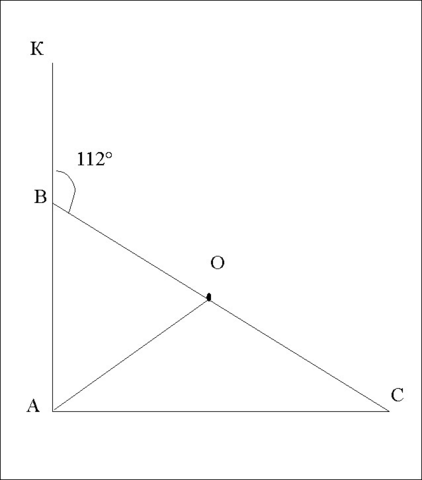
Дано:
ΔАВС-прямоугольный;
∠КВС - внешний;
∠КВС = 112°
∠С - острый;
АО - медиана
Найти ∠АОС
Решение.
1) ∠КВС - смежный с углом ∠АВС.
Сумма смежных углов равна 180°.
∠КВС + ∠АВС = 180°
Отсюда , находим величину ∠АВС.
∠АВС = 180° - 112° = 68°.
∠АВС = 68° - острый.
2) По условию ∠С - острый.
Значит, ∠А - прямой
∠А = 90°
3) Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
∠А + ∠С = ∠КВС
90° + ∠С = 112°
°С = 112° - 90°
∠С = 22°
4) АО - это медиана, проведенная к гипотенузе.
Используем ее основное свойство, согласно которому медиана, проведенная к гипотенузе равна половине гипотенузы.
Получается, что
АО = ОВ = ОС
5) В равнобедренном ΔАОС против равных сторон АО=ОС лежат равные углы:
∠ОАС = ∠С = 22°
6) Сумма всех углов треугольник равна 180°.
Для ΔАОС эта сумма выглядит так:
∠ОАС + ∠С + ∠АОС = 180°
22° + 22° + ∠АОС = 180°
∠АОС = 180° - 44°
∠АОС = 136°