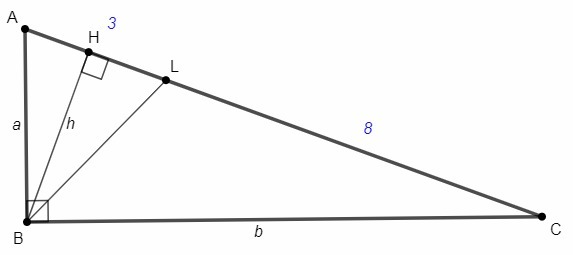
AB=a, BC=b, BH=h
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
a/b=3/8 <=> a=3/8 *b
a^2 +b^2 =11^2 <=>
(3/8 *b)^2 +b^2 =11^2 <=>
b^2(9/64 +1)=11^2 <=>
b=√(11^2*64/73)=88/√73
Приравниваем площади, выраженные через произведение катетов и через гипотенузу (AL+CL=11) и высоту к ней:
ab/2=11h/2 <=> h=ab/11
h=3/8 *88/√73 *88/√73 :11 =3*88/73 =3,62
S(ABL)= AL*h/2 =3*3,62/2 =5,43
--------------------------------------------
В общем виде: AL=x, CL=y
a/b=x/y <=> a=x/y *b
a^2 +b^2 =(x+y)^2 <=>
b^2(x/y +1)^2 =(x+y)^2 <=>
b= (x+y)y/√(x^2+y^2)
ab/2=(x+y)h/2 <=> h=ab/(x+y)
h= xy(x+y)/(x^2+y^2)