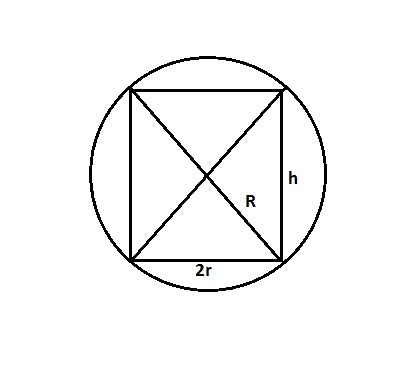
На рисунке осевое сечение шара с радиусом R и цилиндра с радиусом основания r и высотой h
Попробую выразить V цилиндра как функцию от r, для этого мне нужно h выразить через r
(2R)^2=h^2+(2r)^2; h^2=4R^2-4r^2; h=√(4*18.8^2-4r^2)=2√(18.8^2-r^2)
V=pir^2*2√(353.44-r^2)
V`=2pir(2√(353.44-r^2)-r^2/√(353.44-r^2)
приравнивая V`к нулю, получу
2√(353.44-r^2)=r^2/√353.44-r^2)
r^2=235.6; r≈15.35
h=2√(353.44-235.6)≈21.7