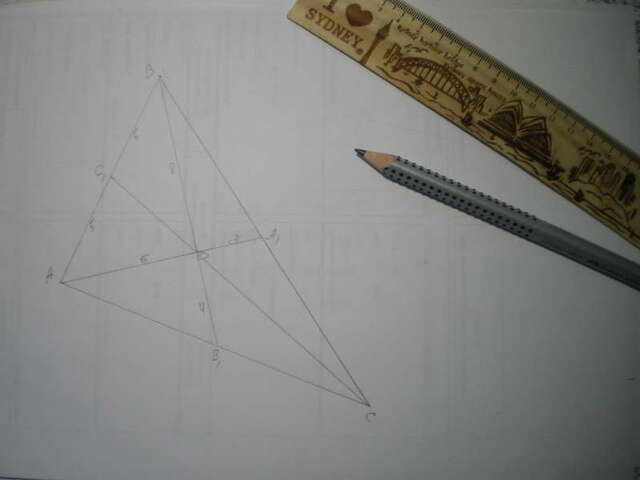
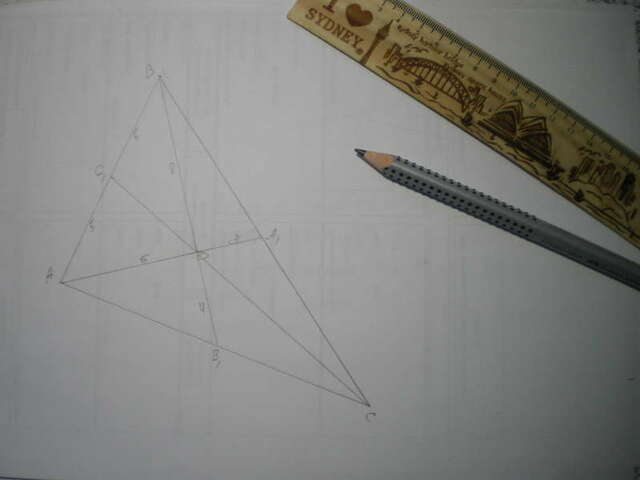
Дано: Δ АВС, АВ=10, АА₁=9, ВВ₁=12.
Найти S(АВС), СС₁.
Решение:
Применяем теорему: медианы треугольника в точке пересечения
делятся в отношении 2:1, считая от вершины.
Следовательно, АО=6, ОА₁=3; ВО=8, ОВ₁=4.
Рассмотрим Δ АВО - прямоугольный,
"египетский", (т.к. стороны кратны 3, 4 и 5).
S(ABO)=1\2 * 6 * 8=24 (ед²)
S(ABO)=S(BOC)=S(AOC) (по свойству медиан треугольника)
S(ABC)=24*3=72 (ед²)
Δ АОВ - прямоугольный, ОС₁ - медиана, ОС₁=1\2 АВ (по свойству
медианы прямоугольного треугольника); ОС₁=5.
ОС₁=5*2=10; СС₁=5+10=15 (ед)