6)
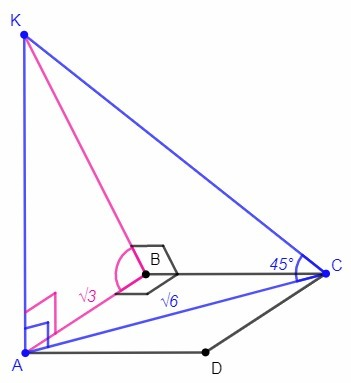
ABCD - прямоугольник, диагонали прямоугольника равны.
AC=BD=√6 (см)
Отрезок КА перпендикулярен плоскости ABC, следовательно перпендикулярен любой прямой в этой плоскости.
КА⊥AC, ∠KAC=90°
Угол между прямой и плоскостью - это угол между прямой и ее проекцией на плоскость. КА⊥(ABC), точка A является проекцией точки K на плоскость ABC, прямая AC является проекцией прямой KС на плоскость ABC, угол между прямыми КC и AC (∠KCA) является углом между прямой KC и плоскостью ABC.
∠KCA=45°
Треугольник KAC - прямоугольный с углом 45°, следовательно равнобедренный.
KA=AC=√6 (см)
Угол между плоскостями (двугранный угол) измеряется углом между перпендикулярами к ребру (линейный угол). Плоскости KBC и ABC пересекаются по прямой BC (ребро двугранного угла).
Плоскость KAB проходит через прямую KA, перпендикулярную плоскости ABC, следовательно KAB перпендикулярна ABC.
(KAB)⊥(ABC)
Прямая KB лежит в плоскости KAB, перпендикулярной плоскости ABC, следовательно KB перпендикулярна ABC и любой прямой в этой плоскости.
KB⊥(ABC), KB⊥BC
AB⊥BC (стороны прямоугольника)
∠KBA - линейный угол двугранного угла между полуплоскостями KBC и ABC.
KA⊥(ABC) => KA⊥AB, ∠KAB=90°
tg(∠KBA)=KA/AB =√6/√3 =√2
∠KBA=arctg(√2) =54,74°