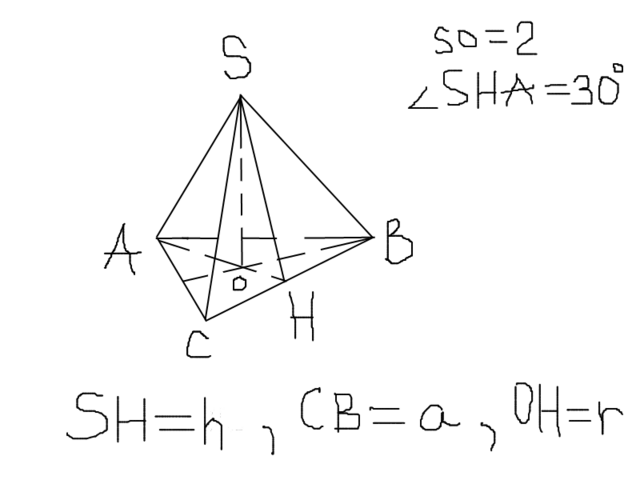
я сделала рисунок, чтобы было понятнее (см. вложение)
пирамида SABC, ее высота SO=2, высота боковой грани SH, биссектриса, медиана и она же высота основания AH, угол SHO=30 градусов(это линейный угол двугранного угла SBCA)
искомая площадь-площадь боковой поверхности, т.е. три площади одной боковой грани:
S=3*0,5*a*h , где a-сторона основания, a=CB,
h-высоты бок. грани, h=SH
найдем SH из треуг. OSH:
катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, т.е.
SH=2*SO=2*2=4 ,т.е. h=4
найдем СB из треуг. ACB:
СB=2*корень(3)*r=2*корень(3)*OH=2*корень(3)*корень(16-4)=2*корень(3)*корень(12)=2*корень(3)*2*корень(3)=4*3=12 ,т.е. a=12
подставляем все значения в первую формулу и получаем:
S=3*0,5*12*4=6*12=72 см^2