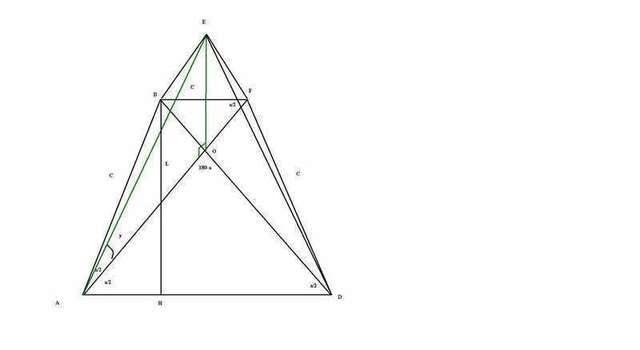
- трапеция равнобедренная ⇒

выходит что угол

так как вертикальные углы. Следует что

, треугольник

равнобедренный .
Так как

диагональ и одновременно биссектриса , угла то угол

,где точка

- пересечений диагоналей (диагонали в равнобедренной трапеций равны) . Опустим с вершины тупого угла высоту

, из прямоугольного треугольник

Пусть