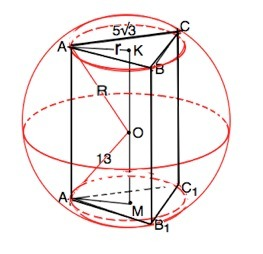
Около призмы можно описать сферу тогда и только тогда, когда призма - прямая, а около её оснований можно описать окружность.
Шар описан около призмы, значит, призма прямая, все её вершины лежат на поверхности шара.
Плоскость каждого из оснований призмы пересекает сферу по окружности, описанной около основания.
Поскольку основания - правильные треугольники, радиус такой окружности равен 2/3 высоты ∆ АВС=а/√3=5 см.
Отрезок КМ, соединяющий центры окружностей, описанных около оснований призмы, параллелен боковому ребру и равен ему. Центр сферы лежит на середине О этого отрезка.
Соединим О с А и К. Т.к. КМ перпендикулярен основаниям призмы, треугольник АКО прямоугольный.
По т.Пифагора КО=√(AO²-AK²)=√(13*-5²)=12 см
АА1=КМ=2КО=24 см
Площадь боковой поверхности прямой призмы равна произведению её высоты на периметр основания.
S=24•3•5√3=360√3 см²